
오늘은 로렌츠 힘 문제를 풀때 간단한 팁을 소개해 드리겠습니다. 로렌츠 힘 문제는 꽤나 흔히 출제되는 유형으로 그 원리만 이해하고 있다면 크게 어렵지 않습니다. 우선 로렌츠 힘이란 자기장 속에서 운동하는 전하가 받는 힘을 말합니다. 그 크기는 자기장의 크기 B, 전하량 q, 전하의 속력 v에 비례하므로 F=qvB로 나타낼 수 있습니다. 다음과 같이 벡터 형식으로도 알아두시면 좋습니다.

그리고 이 힘이 자기장 방향을 축으로 하는 원운동의 구심력 역할을 하게 되어 전하는 반지름이 R인 원운동을 하게 됩니다. 그 힘을 다음과 같이 나타낼 수 있습니다.

위 식을 간단히 정리하여 다음과 같이 나타내면 문제풀이 시 편리합니다.

위 식만 있으면 대부분 로렌츠 힘 문제를 해결할 수 있습니다. 문제는 전하량, 자기장, 반지름, 질량, 속력으로 나타난 위 관계에서 다른 요소가 개입할 때입니다. 다음 문제를 봅시다.

이 문제에서는 원운동의 주기를 묻고 있습니다. 원운동의 주기는 다음과 같이 나타낼 수 있습니다. (이 식은 나중에 보어의 수소원자 모형 할때도 나오니 필히 암기하세요!)
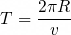
여기서 주기는 R과 v의 비율에 관련됩니다. 처음 식을 적절히 변형하면 B는 v/R에 비례한다는 것을 알 수 있습니다. B=v/R이 2배로 증가했으므로 R/v는 1/2로 감소할 것이고, 따라서 주기는 1/2배가 됩니다. 답은 3번입니다. 여기서 놓치지 말아야 할 게, qBR=mv의 식에서 질량(m), 전하량(q), 자기장(B)는 특별한 언급이 없다면 불변하는 값이고, 반지름(R), 속력(v)은 변할 수 있다는 것입니다. 문제에서 자기장의 세기가 두 배로 커졌다는 언급이 있었고 질량과 전하량에 대해서는 언급하지 않았으므로 이 둘은 변하지 않는다고 생각해야 합니다. 그렇다면 R과 v만 변하기 때문에 주기를 구할 수 있게 됩니다. 이와 비슷한 문제가 또 있습니다.

여기서는 질량, 전하량, 자기장의 변화에 대한 언급이 없으므로 반지름과 속력만 변하게 됩니다. qBR=mv에서 v가 2배가 되므로 R도 2배가 되는데, T=2πR/v는 그대로입니다. 따라서 답은 3번입니다.

이 문제에서는 qBR=mv의 식 말고도 하나의 식이 더 필요합니다. '전위차 ΔV에 의해 가속된 후'라는 표현에서 다음 에너지 전환 식이 필요합니다.

즉, 로렌츠 힘 식과 에너지 식 2가지를 각각 a와 b의 경우에 적용해서 입자 A,B의 질량비를 구해야 하는 문제입니다. 그런데 이렇게 여러 식을 세워서 풀 경우 헷갈리기도 하고 시간도 오래 걸리게 됩니다. 그래서 좀더 깔끔하게 푸는 방법이 없을까 고민해 보았습니다. 우선 a의 경우 모든 물리량이 기본값입니다.(q, m, v, B, R, ΔV 등) b의 물리량은 a의 물리량에 비해 몇 배가 되었는지만 계산하면 됩니다.
우선 구하고자 하는 것이 질량비이므로 b의 질량이 a의 x배라고 합시다. 에너지 식을 보면 전하량 q는 b가 2배입니다. 전위차 ΔV는 동일하므로 속력 v는 b가 a의 √(2/x)배가 됩니다. 이 관계를 식으로 쓰면 다음과 같습니다.

이것을 qBR=mv의 식에 적용하여 봅시다. 자기장 B는 동일하고, 전하량 q와 반지름 R은 b가 각각 a의 2배입니다. 이를 식으로 쓰면 다음과 같습니다.


따라서 답은 4번입니다. 이렇게 단 세 줄의 식으로 문제를 풀 수 있습니다. 이 방식을 쓰면 잘 헷갈리지도 않게 되고 다른 로렌츠 힘 문제를 풀때도 유용한 팁이니 참고하시길 바랍니다!
'실전풀이&예상문제 > [물리학개론 실전풀이]' 카테고리의 다른 글
| 【물리학개론】정상파·공명·맥놀이 고난도 문제 풀이법 (0) | 2021.12.31 |
|---|---|
| 【물리학개론】축전기와 에너지 문제 접근법 (2) | 2021.12.30 |
| 【물리학개론】전기장 적분 스피드 해법 (0) | 2021.12.28 |
| 【물리학개론】축전기 옮기기 문제 접근법(feat.문제오류?) (1) | 2021.12.27 |
| 【물리학개론】복잡한 형상의 저항 구하기 (1) | 2021.12.25 |





댓글