
이제 어느덧 전자기학 파트로 넘어왔네요~ 역학 파트에서 아직 다루지 못한 주제들도 몇 가지 있는데 추후에 완성도를 높여 업로드 할 계획입니다! 오늘은 전자기학에서 아~주 가끔씩 출제되었던 전기장 적분 문제들을 다뤄보겠습니다(여기서는 전기장을 적분하여 전위를 구하는 문제가 아닌 전하요소를 적분하여 전기장을 구하는 문제를 말합니다.) 7급에서는 11년도 지방직에서만 출제되었습니다.
오늘 알려드릴 풀이는 다분히 실용적인 측면에서 알려드리는 것입니다. 전기장 적분 문제는 풀이도 엄청나게 길고 난이도도 상당합니다. 전기장 적분 문제를 각잡고 정확하게 풀려면 온갖 유형들을 철저히 연습하지 않는 이상 2~3분은 걸린다고 생각합니다. 1문제를 1분 내에 풀어야 하는 공무원시험 특성상 비효율적이죠. 특히 적분요소를 설정하고 전하를 전하밀도로 바꾸고 하다보면 실수도 많이 나오기 때문에 사실 전기장 적분 문제가 나오면 스킵하시길 권장드립니다.
그러나, 혹시나 시간이 남아서 건드려보고자 하는 상황이 올수도 있습니다. 제가 알려드릴 풀이는 시간도 1분 내로 걸리면서 맞힐 확률을 조금이라도 높이기 위한 전략적 풀이라고 보시면 되겠습니다. 또한 지금까지 출제된 7급, 기술고시, 변리사 문제들에 한해서는 유효한 풀이기도 합니다!
우선 어떤 문제부터 보도록 하겠습니다.

먼저 정석적인 풀이는 다음과 같습니다.
각 점에서 발생하는 전기장의 세기

이 때 전하밀도는

그림을 보시면 y방향(세로방향)으로 대칭적이기 때문에 전기장의 y축성분은 서로 상쇄되고 x축성분만 남게 되는 것을 알 수 있습니다. x축성분은 Ecosθ입니다. 또한 l=Rθ이므로 dl=Rdθ입니다. 따라서 적분식을 다음과 같이 쓸 수 있습니다.

위 식을 0에서 π/3까지 적분하고 이를 2배 해주면 다음과 같이 구하고자 하는 전기장의 세기가 나옵니다.

으로 답은 4번입니다. 실전에서 처음보는 문제를 이런식으로 풀 수 있을까요? 저는 불가능하다고 봅니다. 이러한 문제를 빠르게 해결하기 위해서는 선지 구성에 주목해야 합니다. 선지를 보면 kQ/πR²는 공통적으로 포함되어 있고 앞의 계수들만 다릅니다. 즉 앞의 계수들만 알면 답을 고를 수 있다는 것인데, 그렇다면 계수가 어떻게 달라질 수 있는지를 알아야 합니다. 저는 계수에 영향을 주는 요인을 3가지로 나누어 보았습니다.
i) 적분요소
적분요소는 무한히 작은 전하 요소들이 각자 얼만큼의 전기장을 형성하는 지를 나타냅니다. 전기장을 작은 요소들로 분해해 보면, 각자가 kq/R²의 전기장을 형성하는 것을 알 수 있습니다. 이는 쿨롱상수, 거리에 의해 정해집니다. 위 문제에서는 쿨롱상수, 거리 모두 특별한 점이 없이 없으므로 1이라고 하겠습니다.
ii) 전하밀도
위 문제에서 전하 Q가 길이 2πR/3인 원호에 분포되어 있습니다. 따라서 전하밀도에 의한 계수는 2π/3의 역수입니다. 전하밀도는 주로 문제 조건을 보면 알 수 있습니다.
iii) 적분값
실질적인 적분에 의해 계수가 바뀌는 것을 말합니다. k, q, r 등은 적분요소에 따라 일정하므로 적분해도 변하지 않는 것을 이용한 것입니다. 위 문제에서 실질적인 적분이 이루어지는 것은 cosθ뿐입니다. 따라서 cosθ를 0에서 π/3까지 적분한 값의 2배, 즉 √3이 됩니다. 적분값은 주로 주어진 기하학적 형상에 의해 결정됩니다.
위 3가지 요소를 모두 곱한 값, 즉 1×(3/2π)×√3의 값을 계산해보면 4번이 답이 되는 것을 볼 수 있습니다. 각 요소에 대한 정의가 엄밀하지 않아서 헷갈릴 수 있을텐데 다른 문제를 통해 더 알아보겠습니다.

이 문제는 정량적 계산을 요구하지 않기 때문에 답 자체는 쉽게 구할 수 있습니다. 이전 문제와 비슷하게 x축방향은 상쇄되고 y축방향으로 작용하여 (a)와 (b)에서 방향은 같습니다. 또한 (b)에서는 코사인이 곱해져 적분되므로 한 점에 몰려있을 때보다 그 크기가 더 작아지므로 답은 1번입니다. 이번에는 아까 소개한 방식을 적용해서 실제 전기장을 계산해 보겠습니다.
적분요소 - k, r에 특이한 점이 없으므로 1
전하밀도 - Q가 길이 πr에 분포되어 있으므로 1/π
적분값 - cosθ를 -π/2~+π/2까지 적분하므로 2
따라서 (b)에서 전체 전기장은 2kQ/πr²입니다. (a)에서는 kQ/r²이므로 (b)에서 더 작은 것을 알 수 있습니다. 실제 값과 일치하는지 보기 위해 정확한 계산 과정도 보여드리겠습니다.


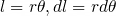

대충 감이 오시나요? 변리사 문제들을 통해 다른 문제들도 풀어보겠습니다.

적분요소 - 쿨롱상수가 9
전하밀도 - 3(문제 조건)
적분값 - -0.25m~0.25m는 상쇄됨. 1/r²를 0.25에서 0.75까지 적분하므로

9×3×(8/3)=72입니다. 유효숫자만 구하면 되므로 단위는 크게 신경쓰지 않아도 됩니다. 답은 4번입니다!

적분요소 - 거리가 √5이므로 역수의 제곱인 1/5가 곱해져야 하고 그중에서도 수직(코사인)성분만 고려하므로 2/√5도 곱해야함.
전하밀도 - Q가 2πR에 분포해 있으므로 1/2π
적분값 - 한바퀴 적분하므로 2π
따라서 다음과 같이 값이 나옵니다.

4번으로 답이 나오는데 실제로도 답은 4번입니다. 전기장 적분 문제에서 1)적분요소 2)전하밀도 3)적분값 이 세가지만 기억한다면 이렇게 간단한 계산만으로 선지에서 답을 골라낼 수 있게 됩니다. 이러한 방법으로도 답이 나오는 이유는 전기장의 적분이 비교적 간단한 상황에서 이루어지기 떄문입니다.(직선, 원형 등) 그런데 여기서 상황이 더 복잡해지면 이 방법을 쓸 수 없게되나 정석적인 풀이 과정은 더욱 어렵고 복잡해져 사실상 푸는 사람이 없게 될겁니다. 그러한 방식으로는 출제되지 않는다고 가정한다면 꽤나 쓸만한 방식이지 않나 싶습니다.
오늘 설명한 내용들은 아무래도 제가 만들어낸 개념이기도 하고 설명이 엄밀하지 않은 부분이 있기 때문에 이해가 잘 되지 않는다면 그냥 패스해도 무방하다고 봅니다~!
'실전풀이&예상문제 > [물리학개론 실전풀이]' 카테고리의 다른 글
| 【물리학개론】축전기와 에너지 문제 접근법 (2) | 2021.12.30 |
|---|---|
| 【물리학개론】로렌츠 힘 문제 간단하게 푸는법 (2) | 2021.12.29 |
| 【물리학개론】축전기 옮기기 문제 접근법(feat.문제오류?) (1) | 2021.12.27 |
| 【물리학개론】복잡한 형상의 저항 구하기 (1) | 2021.12.25 |
| 【물리학개론】단진자 최저점에서의 장력 (0) | 2021.12.25 |





댓글