
전달함수와 정상상태오차 문제들을 보시느라 수고 많으셨습니다. 오늘은 그것들에 비하면 간단한 팁 정도의 내용을 다뤄보겠습니다. 대부분의 문제에서는 임펄스응답, 계단응답, 램프응답 등에 대한 응답을 f(t) 또는 F(s)로 표현되는 수식으로 답을 도출하기를 요구합니다. 그런 경우에는 수식을 직접 계산하는 방법밖에 없고, 오래 걸릴 수도 있습니다. 하지만 어떤 문제들에 대해서는 단지 그것의 값의 존재 여부나 수식의 형태만을 묻기도 합니다. 그러한 문제들의 경우 수식을 직접 계산할 필요 없이 형태만을 눈으로 읽고 답을 도출할 수 있습니다. 오늘은 그러한 문제 유형과 방법에 대해 알아보도록 하겠습니다.
보통 2차 시스템이라 하면 다음과 같은 형태를 가지고 있습니다.

여기서 분모에 해당하는 부분을 특성방정식이라 하는데, 이 특성방정식의 형태에 따라 라플라스역변환을 했을 때 시간응답이 다양한 형태로 나오게 됩니다. 아래 그림을 참조하시길 바랍니다.
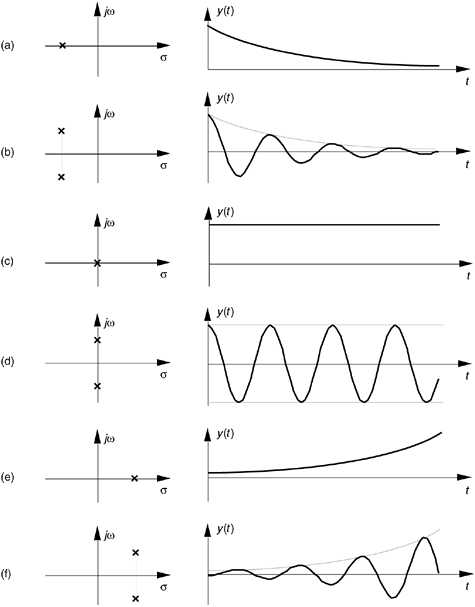
(a)의 경우, 특성방정식이 두 실근 또는 중근을 가질때, 즉 a>0이고 판별식 D≥0일 때입니다.(D=a²-4b) 과감쇠(overdamped)이고, 안정(stable)하며, 시간응답은 지수감쇠 형태(e^-wt)로 나타납니다. 특히 D=0일때는 critically damped라고 합니다만 D>0일 떄와 큰 차이는 없습니다.
(b)에서는 특성방정식이 두 허근을 가질 때, 즉 a>0이고 판별식 D<0일 때입니다. 부족감쇠(underdamped)이고, 이 역시 안정(stable)하며, 시간응답은 지수감쇠에 사인/코사인이 곱해진 형태로 진동하면서 그 진폭이 점점 감소하는 형태입니다.
(c)는 a=b=0일때이며 응답이 상수로 나타납니다.
(d)는 a=0일때 입니다. 무감쇠(undamped)이고 임계안정(marginally stable)하며 시간응답은 사인 또는 코사인 함수입니다.
(e)는 a<0이면서 판별식 D≥0일 때입니다. 불안정(unstable)하며 시간응답은 지수함수 형태로 무한대를 향해 발산합니다.
(f)는 a<0이면서 판별식 D<0일 때입니다. 불안정(unstable)하며 시간응답은 발산하는 지수함수에 사인/코사인이 곱해진 형태로 진동하면서 그 진폭이 점점 커지면서 마찬가지로 발산합니다.
| 그림 | 특성방정식 | a,b | D=a²-4b | 감쇠 | 안정 | 시간응답 |
| (a) | 두 실근 | a>0 | D>0 | 과감쇠 (overdamped) |
안정 (stable) |
지수감쇠 |
| 중근 | a>0 | D=0 | 임계감쇠 (critically damped) |
|||
| (b) | 두 허근 | a>0 | D<0 | 부족감쇠 (underdamped) |
지수감쇠하면서 진동 | |
| (c) | s² | a=b=0 | D=0 | 무감쇠 (undamped) |
임계안정 (marginally stable) |
상수 |
| (d) | s²+b | a=0 | D<0 | 정현진동 | ||
| (e) | 두 실근 | a<0 | D>0 | - | 불안정 (unstable) |
발산 |
| (f) | 두 허근 | a<0 | D<0 | - | 진동하면서 발산 |
1차 시스템은 더 간단합니다. k/(s+a)에서 a>0이면 시간응답은 지수감쇠하며 안정하고, a<0이면 시간응답은 지수발산하며 불안정합니다. a=0이면 시간응답은 상수입니다.
위 내용들을 모두 숙지하셨다면, 다음 성질도 이해할 수 있어야 합니다. 어떤 전달함수 G(s)에 대하여 그것에 신호 R(s)가 주어졌을 때 응답 Y(s)는 G(s)R(s)와 같습니다. 이 때 R(s)가 단위임펄스, 단위계단, 단위램프일 때 시간응답은 서로 미분/적분 관계에 있습니다. 이 관계를 아래와 같이 나타낼 수 있습니다.

즉 어떤 전달함수 G(s)에 대하여 단위계단응답 y(t)=t라면 단위임펄스응답은 그것을 t에 대해 미분한 1, 단위램프응답은 그것을 t에 대해 적분한 t²/2+C(C는 상수)가 된다는 것입니다. 위 내용을 모두 이해했다고 가정한 후 다음 문제를 풀어보겠습니다.

위 문제를 정석적으로 풀기 위해서는 주어진 G(s)의 식에 1/s를 곱한 후 역라플라스변환을 통해 시간응답 y(t)를 구하는 과정을 거쳐야 합니다. 하지만 위 문제에서는 최종치의 존재 여부만을 물었을 뿐, 그 값을 구할 필요는 없습니다. 또한 문제에서 단위계단응답의 최종치를 구하라고 했으므로 t→∞일 때 단위계단응답의 값, 즉 단위임펄스응답을 무한대까지 적분한 값을 구하면 됩니다.
우선 ㄱ을 보면 a>0이고 D=a²-4b>0이므로 위 표에서 (b)의 경우에 해당합니다. 지수감쇠하며 진동하는 함수는 0으로 수렴하며, 그것을 무한대까지 적분하게 되면 그것은 특정한 값에 수렴하게 됩니다. 따라서 최종치가 존재한다고 볼 수 있습니다.(D=0이거나 D<0인 경우에도 무한대까지 적분하게 되면 일정 값에 수렴하기 때문에 최종치는 여전히 존재합니다.)
ㄴ을 보면 a=0이므로 (d)의 경우에 해당합니다. 정현진동(sin, cos)의 경우 그것을 적분해도 그대로 정현진동하게 되고, 무한대로 적분한다 해도 계속 진동하게 됩니다. 따라서 최종치가 존재하지 않습니다.
ㄷ을 보면 a<0이므로 (e),(f)중 하나에 해당합니다. 어차피 둘 다 발산하므로 그것을 무한대까지 적분했을때의 값 역시 발산할 것이며 최종치가 존재하지 않습니다.
따라서 위 문제의 경우 전달함수 분모의 s의 일차항의 계수값 부호만 보고 정답을 판별할 수 있습니다. 답은 1번입니다.

ㄱ의 경우 a<0이므로 발산합니다. 무한대까지 적분했을 때 역시 발산하므로 정상상태오차는 존재하지 않습니다.
ㄴ의 경우 a=0이므로 무감쇠(정현진동)이고, 무한대까지 적분했을 때 계속 진동하므로 정상상태오차는 존재하지 않습니다.
ㄷ의 경우 a>0이므로 무한대까지 적분했을 때 특정 값에 수렴합니다. 최종값 정리를 쓰면 다음과 같습니다.

최종값 y_ss=1이고 e_ss=1-y_ss이므로 정상상태오차는 0입니다. 따라서 답은 2번입니다. 위 문제의 경우 ㄱ, ㄴ만으로 이미 선지를 고를 수 있으므로 사실상 5초컷이 가능했던 문제였습니다!

위 문제도 따로 라플라스변환을 구할 필요가 없습니다. 임펄스응답을 물었고 극점이 -5, 0에 위치해 있으므로 각각 지수감쇠, 상수이므로 답은 2번입니다.

위 문제도 비슷한 유형입니다. p1,2는 지수감쇠하며 진동하고, 단위계단응답을 물었으므로 이를 적분하기 때문에 상수가 추가되어 답은 4번의 형태입니다. 참고로 영점 z=-10은 문제를 푸는 데 아무 관련 없는 조건입니다.
'실전풀이&예상문제 > [자동제어 실전풀이]' 카테고리의 다른 글
| 【자동제어】이득여유(GM) & 위상여유(PM) 문제의 접근법 (1) | 2022.01.26 |
|---|---|
| 【자동제어】RH 판별법 모든 경우의수 총정리! (0) | 2022.01.25 |
| 【자동제어】정상상태오차 완전정복 - 3 (3) | 2022.01.22 |
| 【자동제어】정상상태오차 완전정복 - 2 (4) | 2022.01.21 |
| 【자동제어】정상상태오차 완전정복 - 1 (0) | 2022.01.20 |





댓글