
이전 포스팅에서 입력오차이며 비단위피드백시스템이고 블록선도에 E(s)가 표시되어 있지 않을 때까지 했습니다. 그런데 이 경우 계산법이 또 한가지 있습니다.
2-3) 입력오차, 비단위피드백 시스템, 블록선도 상 E(s) 존재하지 않음 : 단위피드백시스템 변환
저번에 했던 'E=R-Y 계산법' 대신, 비단위피드백시스템을 단위피드백시스템으로 변환한 후 오차상수법을 이용하는 방법도 있습니다. 개인적으로는 E=R-Y의 방법이 더 빠르다고 생각하나 이 방법도 알아두시면 좋을 것 같아 소개해드리겠습니다.

위 비단위피드백시스템 형태를

단위피드백시스템 형태로 바꾸었을 때 개루프함수 G'(s)는 다음과 같이 나타납니다. G'(s)=(바깥곱)/(분모곱+분자곱), 단 H(s)-1을 기준으로 계산(이 내용에 대한 것은 【자동제어】"계산 없이" 전달함수 구하는 방법 - 2 를 참고하세요!)
이렇게 구한 G'(s)로 오차상수법을 쓰면 됩니다. 이 방법을 이용해서 다음 문제를 풀어보겠습니다.



0형 시스템이므로 정적위치오차상수와 정상상태오차는 다음과 같습니다.

따라서 답은 2번입니다. E=R-Y 방법으로도 한번 구해보면 다음과 같습니다.


전과 동일한 결과가 나옵니다. 둘 다 유효한 방법인데 왜 굳이 방법을 여러 개 소개하느냐? 하면 위 2019 서울시 문제의 출제 의도때문입니다. 왜 굳이 불필요하게 H(s)를 s+2와 단위피드백의 형태로 나타냈을 지를 생각해보면, 위와 같이 H(s)-1(=s+2)을 사용하여 단위피드백시스템으로 변환한 후 오차상수법으로 계산하는 것을 의도했음을 알 수 있습니다. 또한, 위 문제의 선지를 보면 r(t)가 δ(t), 1, t, t²일 때를 각각 묻고 있습니다. 단위피드백시스템으로 변환하게 되면 개루프함수 G'(s)의 형(type)을 알 수 있고, 위의 경우에는 0형 시스템이므로 r(t)=1일 때 정상상태오차 값이 나타난다는 것을 바로 알 수 있습니다. 하지만 E=R-Y를 계산하게 되면 개루프함수를 바로 알 수 없고 별도로 계산해 주어야만 시스템의 형(type)을 알 수 있습니다. 따라서 위와 같이 어떤 입력(계단, 램프, 포물선..)에 대해 정상상태오차값이 나타나는지를 바로 알기 위해서는 단위피드백시스템으로 변환하는 방법을 사용하여야만 합니다.
3) 외란에 대한 정상상태오차
우선 외란에 대한 정상상태오차를 구할 때에는 오차상수법은 사용하지 않습니다. 물론 오차상수법과 동일한 방식으로 식을 세워서 풀 수는 있지만, 그보다는 전달함수 Y(s)/D(s)를 계산하는 것이 더 빠르다고 판단됩니다.
3-1) 외란오차, 단위피드백시스템일 때 / 비단위피드백시스템이면서 블록선도에 E(s)가 존재하지 않을 때
외란오차의 경우 정상상태오차를 블록선도로부터 직접 구해야 합니다. 먼저 단위피드백시스템일 때는 다음과 같습니다.

E(s)=R(s)-Y(s)에서 R(s)=0이므로 E(s)=-Y(s)입니다. 따라서 다음 식과 같이 정상상태오차를 구합니다.


또한, 비단위피드백시스템이라 할지라도 블록선도에 E(s)가 없다면 E(s)=R(s)-Y(s)로 계산하므로 위와 동일하게 계산됩니다. 다만 비단위피드백시스템+외란오차의 조합은 출제된 적이 없습니다. 그렇다면 문제를 풀어보도록 하겠습니다.
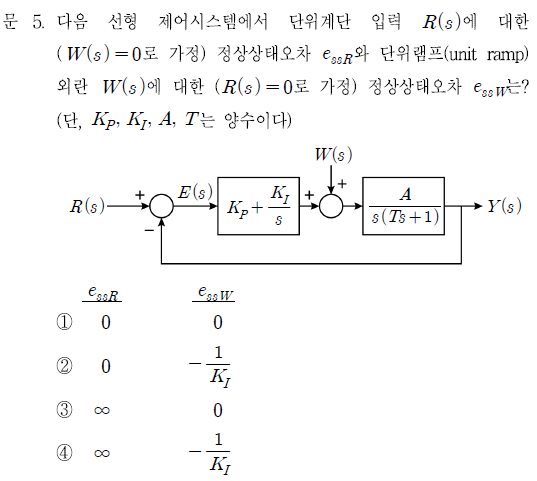
우선 W(s)에 대한 정상상태오차부터 구해보도록 합시다. 전달함수 Y(s)/W(s)를 구해보면 다음과 같습니다.

정상상태오차 e_ssW는 다음과 같이 구할 수 있습니다.


여기서 만약 외란신호 W(s)가 단위계단 신호라면 sW(s)=1이 되고 W(s)가 단위램프 신호라면 sW(s)=1이 되므로 위처럼 lim식을 세울 필요 없이 전달함수에서 바로 정상상태오차 -1/KI을 구할 수 있습니다. 이것을 'E=-Y 계산법'이라고 하겠습니다. 이전에 포스팅했던 'E=R-Y 계산법'처럼 과정을 간단히 한 것입니다.

다음으로 R(s)에 대한 정상상태오차를 구해보겠습니다. 그런데 개루프함수가 2형이고 단위계단 입력이므로 정상상태오차는 0인 것을 알 수 있습니다. 그래도 한번 구해 보겠습니다. 전달함수는 다음과 같습니다.

정상상태오차 e_ssR는 다음과 같습니다.
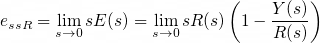

3-2) 외란오차, 비단위피드백시스템이면서 블록선도에 E(s)가 존재할 때
비단위피드백시스템에서 블록선도에 E(s)가 없다면 E(s)=R(s)-Y(s)로 계산하므로 위와 동일합니다. 그러나 아래와 같이 블록선도에 E(s)가 존재할 경우, E(s)=R(s)-Y(s)H(s)=-Y(s)H(s)이므로 다음과 같이 계산해야 합니다. 앞에서 말씀드렸듯 비단위피드백시스템+외란오차의 경우는 출제된 적이 없습니다.


여기까지 모든 방법에 대해 알아보았습니다. 지금까지의 내용을 종합하여 알고리즘으로 나타내 보았습니다. 그러나 실전 상황에서 아래와 같은 표를 떠올리면서 문제를 풀 수는 없습니다. 어느 조건에서 어느 방법을 써야 하는지를 기출문제를 반복해서 풀어봄으로써 기계적으로 떠올릴 수 있도록 체화하는 과정이 필요한 이유입니다.
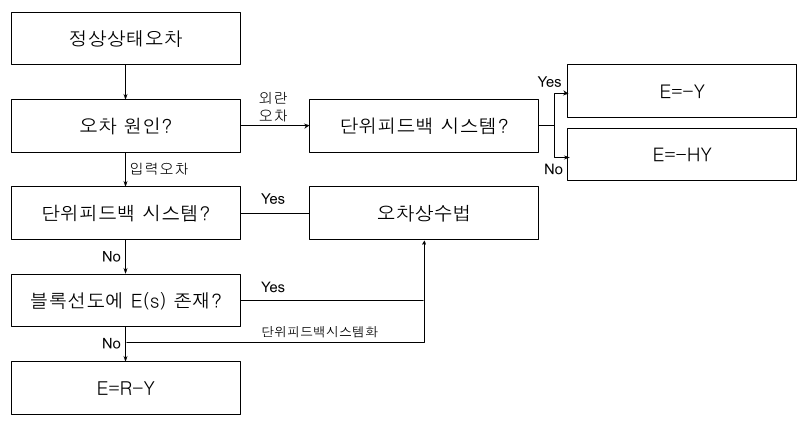
다음 시간에는 정상상태오차 관련 기출문제를 풀면서 방법을 더 익혀보도록 하겠습니다~!
'실전풀이&예상문제 > [자동제어 실전풀이]' 카테고리의 다른 글
| 【자동제어】시간응답의 성질을 이용해 눈으로 풀기 (0) | 2022.01.23 |
|---|---|
| 【자동제어】정상상태오차 완전정복 - 3 (3) | 2022.01.22 |
| 【자동제어】정상상태오차 완전정복 - 1 (0) | 2022.01.20 |
| 【자동제어】"계산 없이" 전달함수 구하는 방법 - 2 (2) | 2022.01.19 |
| 【자동제어】"계산 없이" 전달함수 구하는 방법 - 1 (3) | 2022.01.18 |





댓글