
저번 시간에는 단위피드백 시스템, 비단위피드백 시스템, 외란오차 시스템, 루프 전에 이득이 존재하는 시스템의 폐루프 전달함수를 계산 없이 구하는 방법에 대해 알아보았습니다. 오늘은 위 4가지 꼴에 해당하지 않는 경우에도 적용할 수 있도록 일반화하여 전달함수를 구하는 법을 알아보겠습니다.
5) 블록선도에서 전달함수 구하기 일반화
다음과 같은 단계로 이루어집니다.
i) 모든 분모의 곱을 구한다.
ii) Loop 1,2,3...을 설정한다.
iii) Loop 1의 내 분자와 Loop 1외 분모를 곱한다. Loop n까지 반복한다.
iv) 전방경로에 존재하는 분자와 전방경로 외 분모를 곱한다.
v) i)~iii)을 분모에, iv)를 분자에 쓴다.
vi) 만약 비접촉루프가 존재한다면, 분자를 곱하여 분자 또는 분모에 추가한다. (단 지금까지 기출된 부분에서 제어함수 G(s)가 주어진 상태에서 비접촉루프가 있는 블록선도를 제시한 경우는 없었습니다.)
각 단계가 무엇을 의미하는지 올해 출제된 기출문제를 통해 설명드리겠습니다!

우선 D(s)=0일 때 Y(s)/R(s)를 구해 보겠습니다.
i) 모든 분모의 곱을 구한다. → s²입니다.
ii) Loop 1, Loop 2를 다음과 같이 설정할 수 있습니다.

iii) Loop 1 내의 분자(K1s)와 Loop 1 외의 분모(1)을 곱한다. → K1s
Loop 2 내의 분자(K)와 Loop 2 외의 분모(1)을 곱한다. → K
iv) 전방경로 내의 분자(K,1)와 전방경로 외의 분모(1)를 곱한다. → K×1×1=K
v) i)~iii)의 결과를 분모에, iv)의 결과를 분자에 쓴다.

다음으로 R(s)=0일 때 Y(s)/D(s)를 구해 보겠습니다. i), ii), iii)는 이전과 동일합니다. 즉 전방경로가 바뀌면 분자에 해당한는 부분(iv)만 바꿔주면 됩니다.
iv) 전방경로에 존재하는 분자와 경로 외의 분모를 곱한다. → 1
v) i)~iii)의 결과를 분모에, iv)의 결과를 분자에 쓴다.

위 과정에서 곱셈은 머릿속으로도 충분히 가능하니, 바로 전달함수를 구할 수 있습니다. 이를 이용해서 다음 문제를 풀어보겠습니다.

여기서는 안정성을 묻고 있으므로 특성방정식에 해당하는 분모만 구하면 됩니다.
i) 모든 분모의 곱 : s(s²+16s)
ii) Loop 1(안쪽 루프), Loop 2(바깥 루프) 설정
iii) Loop 1 내의 분자곱(8K), 외부의 분모곱(s) / Loop 2의 분자곱(8), 외부의 분모곱(1)
이들을 모두 더하면 s³+16s²+8Ks+8입니다. 바로 RH 판별법을 쓰면 됩니다.

여기서도 분모를 통해 답을 얻을 수 있습니다. G1(s)의 값을 x라 하면,
i) 모든 분모의 곱 : s(s+2)(s+5)
ii) Loop 1(왼쪽 루프), Loop 2(오른쪽 루프) 설정
iii) Loop 1 내의 분자곱(3x), 외부의 분모곱(s+5) / Loop 2의 분자곱(2), 외부의 분모곱(s)
분모(특성방정식)는 s³+7s²+10s+3x(s+5)+2s입니다. 계수비교를 하면 3x+12=24(일차항) 또는 15x=60(상수항)이므로 x=4로 답은 1번입니다.
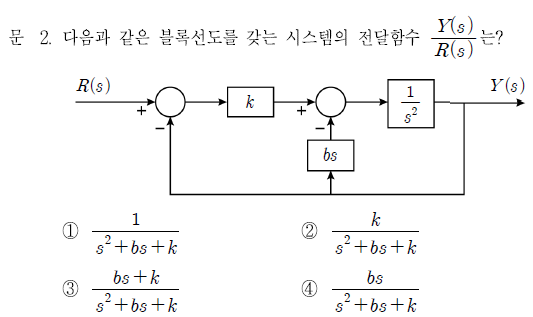
i) 모든 분모의 곱 : s²
ii) Loop 1,2 설정
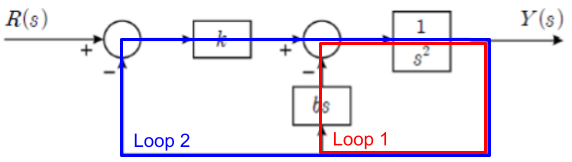
iii) Loop 1 내의 분자곱(bs), 외부의 분모곱(1) / Loop 2의 분자곱(k), 외부의 분모곱(1)
iv) 전방경로 내의 분자곱(k), 외부의 분모곱(1)
v) i)~iii)을 분자에, iv)를 분모에 쓰면 다음과 같이 나오므로 답은 2번입니다.
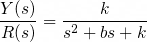
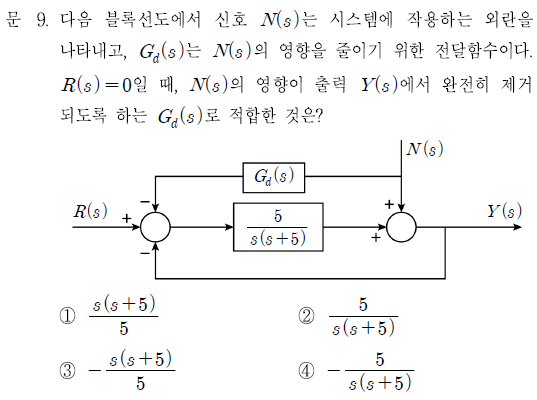
문제에서 R(s)=0일 때 N(s)의 영향이 Y(s)에서 완전히 제거될 조건, 즉 Y(s)/N(s)=0이 될 조건을 물었습니다. 전달함수 Y(s)/N(s)의 분자만 구해서 0을 만들면 됩니다. 여기서는 N(s)→Y(s)의 전방경로가 2가지 존재합니다.
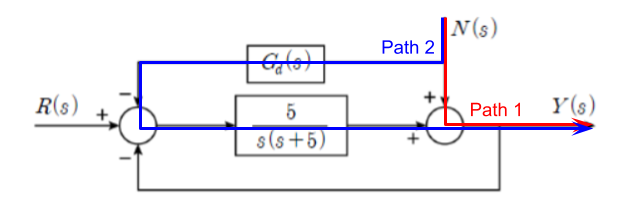
iv) 전방경로 1 내의 분자곱(1), 이외의 분모곱(s(s+5)), 전방경로 2 내의 분자곱(-5Gd(s)), 외의 분모곱(1)
Gd(s)는 다음과 같습니다.
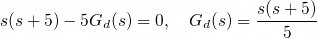
6) 비단위피드백을 단위피드백으로 바꾸기
이것은 비단위피드백 시스템을 등가인 단위피드백 시스템으로 바꾸는 방법인데, 정상상태오차를 구할 때 필요한 경우가 있습니다.
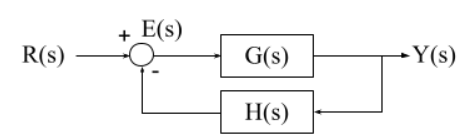
이런 모양의 비단위피드백 시스템을
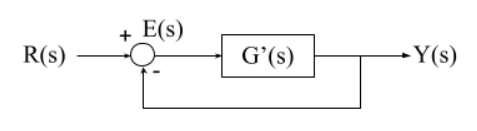
이렇게 바꾸는 것입니다. 이렇게 계산된 새로운 개루프함수 G'(s)에 대해 다음이 성립합니다.
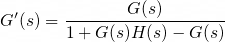
왜 이렇게 나오는지에 대한 유도는 생략하도록 하겠습니다. G(s)=a/A, H'(s)=H(s)-1=b/B라 가정하면 다음과 같이 계산할 수 있습니다.
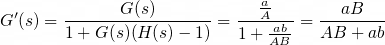
즉, 새로운 개루프함수 G'(s)에 대하여 G'(s)=(바깥곱)/(분모곱+분자곱)으로 계산할 수 있습니다. 단 이 때 H(s)-1을 기준으로 계산하여야 하는 것을 주의하세요.
7) 폐루프시스템을 개루프시스템으로 바꾸기
아주 가끔씩 폐루프시스템을 등가인 개루프시스템을 바꾸어야 할 때가 있습니다. G(s)=(분자곱)/(분모곱-분자곱)입니다.

정상상태오차를 구하기 위해 오차상수법을 쓴다고 가정하면, 먼저 개루프 전달함수 G(s)를 구해야 합니다. (분자곱)/(분모곱-분자곱)을 하면 다음과 같습니다.
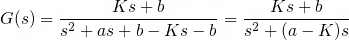
정상상태오차 e=1/Kv이고
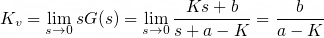
이므로 답은 4번입니다.
오늘 알려드린 내용 역시 처음에는 하다 보면 오히려 기존 방법이 익숙하기 때문에 더 복잡하게 느껴지실 수도 있습니다. 루프 잡는 게 헷갈리고 기존의 방법으로 하는 것이 더 빠르게 느껴진다면 기존의 방법을 쓰셔도 무방합니다. 하지만 저는 이러한 방법으로 전달함수를 구하는 것이 더 깔끔하고 빠르게 느껴졌기 때문에 추천드리는 방법입니다. 여러 기출문제를 통해 반복해서 연습하시다 보면 충분히 익숙해질 수 있을 것입니다. 또한 오늘 푼 문제들 뿐 아니라, 다음에 다룰 정상상태오차 문제들을 풀 때에 큰 도움이 될 것입니다.
'실전풀이&예상문제 > [자동제어 실전풀이]' 카테고리의 다른 글
| 【자동제어】정상상태오차 완전정복 - 2 (5) | 2022.01.21 |
|---|---|
| 【자동제어】정상상태오차 완전정복 - 1 (0) | 2022.01.20 |
| 【자동제어】"계산 없이" 전달함수 구하는 방법 - 1 (3) | 2022.01.18 |
| 【자동제어】역라플라스변환 시 부분분수 전개하는 방법 (1) | 2022.01.16 |
| 【자동제어】그래프가 주어졌을 때 라플라스변환 문제풀이 (4) | 2022.01.15 |





댓글