
오늘은 도플러효과 문제를 다뤄 보겠습니다. 도플러효과 문제들은 그리 어렵지는 않지만 계산이 헷갈릴 때도 있습니다. 계산을 얼마나 돌아가지 않고 깔끔하게 푸느냐가 도플러효과 문제의 관건일 것입니다. 저같은 경우는 도플러효과 공식의 부호가 헷갈리기 때문에 공식에 대입해서 풀기보다는 서로 멀어지거나 가까워짐에 따라 주파수가 증가하거나 감소하는 모습을 머리로 떠올림으로써 문제를 푸는 편입니다.
다음 문제는 제가 도플러효과 문제들 중 까다롭다고 생각했던 문제인데 함께 풀어봅시다.

관측자는 가만히 있고 음원인 소방차만 움직입니다. 음파 속력을 v_s, 소방차의 속력을 v라 하면 다음과 같이 식을 세울 수 있습니다.

소방차가 다가올 때, 주파수가 크게 들릴 것이므로 분모가 더 작아져야 합니다. 따라서 다음과 같습니다.
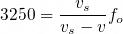
소방차가 멀어질 때, 주파수는 작게 들릴 것이므로 분모가 더 커져야 합니다. 따라서 다음과 같습니다.
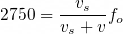
여기서 f_o의 값을 알 수 없으므로, 아래의 식으로 위의 식을 나눠줍니다.
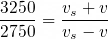
3250=3000+250, 2750=3000-250인 것이 보인다면, 위 식의 좌변은 13/11인 것을 알 수 있을 것입니다. 그에 따라 식을 정리해주면 v=340/12=28.3이 나오는데 단위를 km/h로 바꿔주어야 하므로 36을 곱한 후 유효숫자를 비교해야 합니다. 28×36=1008이므로 100km/h와 비슷합니다. 따라서 답은 4번입니다.
도플러 효과 문제의 경우 죽어라 고민해 봐도 딱히 빠른 풀이법이 떠오르지 않았습니다. 두 대상이 멀어지고 가까워짐에 따른 모습을 그리며 풀면 됩니다. 그런데 몇몇 도플러 효과 문제들 중에는 파동이 반사되어 다시 음원에 도달하는 경우도 있는데, 이러한 경우에는 오히려 공식에 대입해서 푸는 것이 더 효과적입니다. 반사되는 상황은 머리로 한번에 그리기가 어렵기 때문입니다. 다음 문제를 통해 봅시다.

위와 같이 파동이 관측자에 반사되어 음원으로 다시 돌아오는 경우에는 초기 파동과 반사파까지 총 두 번의 계산을 거쳐야 합니다. 그 과정에서 관측자의 속력이 얼마인지, 음원의 속력이 얼마인지, 가까워지는 지 멀어지는 지를 총 두 번씩 생각해야 하기 때문에 번거로울 수 있습니다. 제가 추천하는 방법은 머릿속으로 생각하지 말고, 다음 공식만 떠올리는 것입니다. 이 공식은 음원과 관측자가 같은 방향으로 움직일 때(=둘다 오른쪽으로 간다고 생각) 기준입니다!(부호가 바뀔 수 있습니다)

v_s가 음파의 속력, v_a가 음원의 속력, v_b가 관찰자의 속력입니다. 위 식의 모양을 기억하기는 어렵지 않을 것입니다. 위 문제에서 v_a=v이고, v_b=0이므로 이를 대입하면 다음과 같습니다.

따라서 답은 1번입니다. 보시면 아시겠지만 v_a나 v_b 중 하나가 0이라면 분자와 분모가 서로 약분되는 것을 이용하여 계산을 단축시킬 수 있습니다.
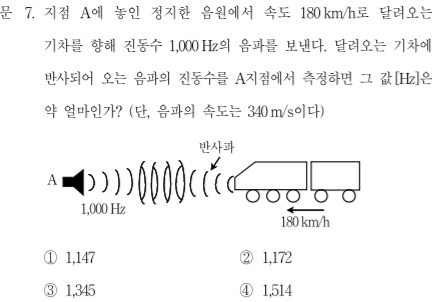
이 문제도 공식을 통해 한방에 풀어 보겠습니다. 180km/h는 50m/s입니다.
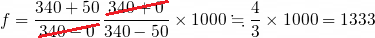
가장 가까운 수인 3번 1,345가 답입니다. 공식을 이용하면 이렇게 한 줄만으로 풀 수 있게 됩니다. 참고로 여기서는 기차가 왼쪽으로 오고 있으므로 부호를 바꾸어 주어야 합니다.

이 문제도 v_b=0이므로 약분되어 다음과 같이 계산됩니다.

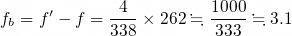
따라서 답은 3번입니다.

이 문제는 다음과 같이 단번에 구해집니다.

따라서 답은 5번입니다.
오늘 내용을 요약하면 일반적인 도플러효과 문제는 기존의 방식대로 풀되, 반사되는 것이 포함된 도플러효과 문제들은 깊이 생각할 필요 없이 공식을 써서 풀 수 있다는 것입니다.
'실전풀이&예상문제 > [물리학개론 실전풀이]' 카테고리의 다른 글
| 【물리학개론】기하광학(거울·렌즈) 문제 풀이 (0) | 2022.01.04 |
|---|---|
| 【물리학개론】굴절과 전반사 간단 풀이법 (0) | 2022.01.02 |
| 【물리학개론】정상파·공명·맥놀이 고난도 문제 풀이법 (0) | 2021.12.31 |
| 【물리학개론】축전기와 에너지 문제 접근법 (2) | 2021.12.30 |
| 【물리학개론】로렌츠 힘 문제 간단하게 푸는법 (2) | 2021.12.29 |





댓글